Flächenberechnung Rechteck
Das Rechteck ist in der Geometrie ein ebenes Viereck, deren Innenwinkel alle rechte Winkel sind, diese ergeben jeweils 90°.
Stell uns deine Frage. Wir antworten dir schnellstens...
Im Gegensatz zum Quadrat, bei dem allen Seiten gleich lang sind, auch gleichseitiges Rechteck genannt, sind beim Rechteck jeweils die gegenüberliegenden Seiten gleichlang. Ein verschobenes Rechteck, es wird zur Seite gekippt, wird dann zum Parallelogramm.
Quelle: Internet Wikipedia
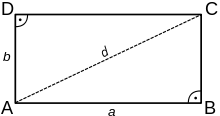
Mit A, B, C und D werden die Winkel abgekürzt, a und b die Seitenlängen und d die Diagonale.
Jedes Rechteck erfüllt immer einige Voraussetzungen, die man sich gut merken kann. Die Summe der Winkel beträgt immer 360°, jeder Winkel einzeln hat 90°. Beide Diagonalen sind gleich lang und halbieren einander. Immer die gegenüberliegenden Seiten sind parallel und gleich lang. Das Rechteck hat einen Umkreis, deren Mittelpunkt der Schnittpunkt der Diagonalen ist.
Beide Symmetrieachsen stehen senkrecht aufeinander, heisst es ist achsensymmetrisch in Bezug auf die Mittelsenkrechten (Seitensymmetralen) der Seiten. Es ist punktsymmetrisch, heisst zweizählig symmetrisch in Bezug auf den Schnittpunkt der Diagonale.
Wie funktioniert der Flächenberechnung Rechner?
Zur Ermittlung der Flächenberechnung müssen mindestens zwei Werte der fünf als Grundlage angegeben werden. Das sind Seite a, Seite b, Fläche, Umfang und Diagonale. Die fehlenden Werte werden dann jeweils berechnet.
Die Werte können mit bis zu zehn Nachkommastellen angegeben werden, mit den Pfeiltasten nach oben oder unten werden diese dann direkt aus einer natürlichen Zahl angezeigt und können entsprechend variiert werden. So wird aus der Zahl 25 mit dem Pfeil nach oben 25,0000000001 usw.
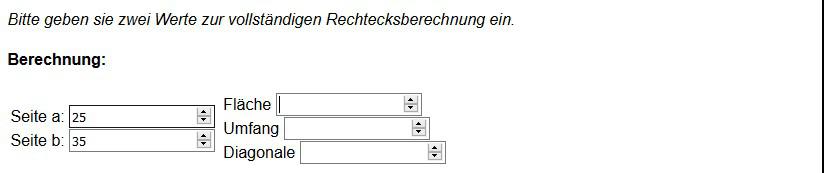
Wir haben das mit einer einfachen Zahl veranschaulicht und haben die Seitenlänge (a) und Seitenbreite (b) ausgewählt.
Das Ergebnis
Je nachdem welche Werte in die Auswahl eingetragen sind, es wird immer das Ergebnis aller Flächen ausgewiesen. Und hier sind auch unsere Ausgangswerte die beiden Seiten a und b direkt an den Anfang gesetzt.

Kennt man die Formeln, so sind die Ergebnisse ganz leicht nachzuvollziehen.
Formeln zur Berechnung beim Rechteck
Zur Berechnung der Flächen liegen Formeln zur Grundlage, diese sind ziemlich einfach und eigentlich geläufig, da man sie schon in der Schule lernt. Die Seitenlänge und Seitenbreite werden immer mit a und b angegeben. Daraus ergeben sich dann folgende einfache Formeln zur Berechnung des Flächeninhalts (A), Umfangs (U), Diagonale (d) und Umkreis (r).
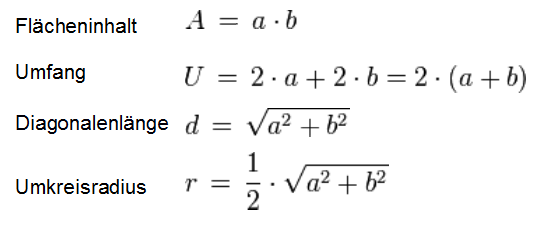
Quelle: Internet Wikipedia
Die Diagonallänge basiert auf dem Satz des Pythagoras a2 + b2 = c2
Dieser ist benannt nach Pythagoras von Samos, er soll diesen mathematischen Beweis als erstes gefunden haben, allerdings ist es doch umstritten, denn die Aussage es Satzes soll schon in Babylon und Indien bekannt gewesen ein, jedoch ohne einen Beweis.
Der Umkreisradius ist die Hälfte der Diagonale, also der Halbe Satz des Pythagoras.
In der Mathematik werden häufig griechische Buchstaben als Kürzel verwendet. Auch die Winkel des Rechteckes werden oft so dargestellt anstatt A, B, C und D. So werden diese dann mit ?, ? = Alpha, ?, ? = Beta, ?, ? = Gamma und ?, ? = Delta benannt.
Bei zusammengesetzten Rechtecken, z.B. bei einer L-Form oder T-Form, wird die Form in zwei Rechtecke unterteilt. Diese werden dann jeweils einzeln berechnet und die Ergebnisse am Ende zusammen gezählt.

