Dodekaeder berechnen
Sie möchten schnell und einfach einen Dodekaeder berechnen lassen? Mit unserem Tool ist das ganz einfach. Tragen Sie dazu nur einen Wert in das entsprechende Feld ein und schon werden für Sie die restlichen Werte ermittelt.
Als Dodekaeder gilt in der Geometrie ein Körper, der sich aus zwölf Flächen zusammensetzt. In den meisten Fällen bezieht sich der Begriff auf einen platonischen Körper mit 12 regelmäßigen Fünfecken. Die Berechnung von typischen mathematischen Größen wie dem Volumen, dem Oberflächeninhalt, oder dem Kantenkugel-Radius folgt bestimmten Formeln. Letztere fallen angesichts der zahlreichen Flächen des Dodekaeders vergleichsweise komplex aus. Aus diesem Grund bietet es sich an, den Dodekaeder Rechner der vorliegenden Seite zu verwenden. Mit dem entsprechenden Tool können Sie die wichtigsten Kennzahlen von einem Dodekaeder berechnen.
Pentagondodekaeder als häufigste Form des zwölfflächigen Körpers
Besteht ein geometrischer Körper aus insgesamt zwölf verschiedenen Flächen, handelt es sich um ein Dodekaeder. Der Pentagondodekaeder stellt eine mögliche Ausprägung der Form dar. Hierbei fällt jede Seite hinsichtlich der Fläche und der Kantenlänge identisch aus. Dementsprechend setzt sich der Pentagondodekaeder aus zwölf regelmäßigen Fünfecken zusammen. Er besitzt 30 gleich lange Kanten. Jede von ihnen bildet eine Seite von zwei verschiedenen Fünfecken. Insgesamt kommt der Körper auf 20 Ecken. In jeder der Ecken treffen drei unterschiedliche Fünfecke zusammen.
Der Pentagondodekaeder gilt als die häufigste Ausprägung des Dodekaeders. Er gehört neben Tetraeder, Hexaeder, Oktaeder und Ikosaeder zu den fünf sogenannten platonischen Körpern. Die Namensgebung geht auf den griechischen Philosophen Platon zurück. Jeder der platonischen Körper besteht aus kongruenten, regelmäßigen Vielecken. Platon beschreibt in seinem Werk „Timaios“ detailliert die fünf unterschiedlichen Körper.
Nützliches Tool – verschiedene Werte vom Dodekaeder berechnen
Die umgangssprachliche Verwendung des Begriffs des Dodekaeders bezieht sich meistens auf den Fall des Pentagondodekaeders. Aus diesem Grund ermittelt der vorliegende Dodekaeder Rechner für Sie stets die mathematischen Größen eines kongruenten Körpers mit zwölf regelmäßigen Fünfecken. Sie finden in dem besagten Tool folgende Eingabefelder vor:
- Kantenlänge a,
- Oberfläche A,
- Rauminhalt V,
- Umkugelradius rU,
- Kantenkugelradius rK,
- Inkugelradius rI,
- Oberfläche zu Volumen (A/V)
Unterhalb der Felder befindet sich zudem ein Auswahlfeld. Dort geben Sie an, auf wie viele Nachkommastellen der Rechner die Ergebnisse rundet.
Dodekaeder Rechner: Eingabe eines Wertes reicht aus
Die aufgezählten Größen stellen in der Geometrie die wichtigsten Kennzahlen zur Beschreibung eines Dodekaeders dar. Allerdings erfolgt deren Berechnung mitunter anhand komplexer Formeln. Die entsprechenden Formeln beinhalten beispielsweise Quotienten, Potenzen oder Brüche. Daher nimmt es einige Zeit in Anspruch, wenn Sie die Größen händisch ausrechnen. Der Einsatz des Rechners auf dieser Seite erleichtert Ihnen den Aufwand erheblich.
Angesichts der Symmetrie des Pentagondodekaeders beinhalten sämtliche Formeln für die Berechnung der genannten Größen lediglich die Kantenlänge als Variable. Das bedeutet im Umkehrschluss: Sie benötigen für den Rechner nur einen Wert. Tragen Sie in eines der Eingabefelder eine Zahl ein und klicken Sie auf „berechnen“. Daraufhin weist Ihnen das Tool die restlichen Werte in den anderen Feldern aus.
Dadurch ergibt sich im Vergleich zur manuellen Berechnung der jeweiligen Formeln mithilfe des Taschenrechners eine erhebliche Zeitersparnis. Eingabe und Rechnung des Tools nehmen lediglich einige Sekunden in Anspruch, ehe Sie sämtliche Ergebnisse sehen. Dagegen tippen Sie in den Taschenrechner jede der komplizierten Formel einzeln ein. Hinzu kommt: Die Größen des Dodekaeders gehören nicht zu den gängigen, bekannten Formeln. Dementsprechend ergibt sich die Notwendigkeit, die formale Rechenweise in einer Formelsammlung nachzuschlagen.
Erläuterung der verschiedenen Werte und Formeln anhand eines konkreten Beispiels
Es bietet sich an, die einzelnen Werte und Formeln anhand eines konkreten Beispiels zu erklären. Im folgenden Beispiel zur Berechnung eines Dodekaeders besitzt der platonische Körper eine Kantenlänge von fünf Zentimetern. Dementsprechend tragen Sie in das vorgesehene Eingabefeld den Wert „5“ ein. Für das Runden der Ergebnisse wählen Sie drei Nachkommastellen aus. Nach einem Klick auf „berechnen“ füllt das Tool die verbleibenden Felder.
Berechnung der Oberfläche des Dodekaeders
Für den Inhalt der Oberfläche gilt folgende Formel:
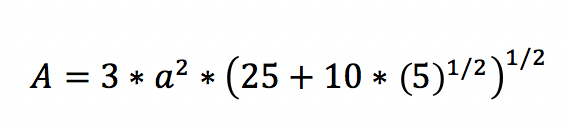
Anstelle der Variable für die Kantenlänge setzt das Tool im Beispiel den gewählten Wert von 5 ein. Nach der Berechnung weist Ihnen der Rechner für die Oberfläche ein Ergebnis von 516,143 cm2 aus.
Volumen gibt Aufschluss über den Rauminhalt des platonischen Körpers
An dritter Stelle im Dodekaeder Rechner befindet sich das Volumen beziehungsweise der Rauminhalt. Im entsprechenden Feld zeigt Ihnen das Tool einen Wert in Höhe von 957,89 cm3 an. Es berechnet sich aus dieser Formel:
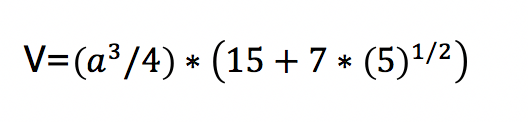
Der Quotient aus den ersten beiden Ergebnissen entspricht der Kennzahl:
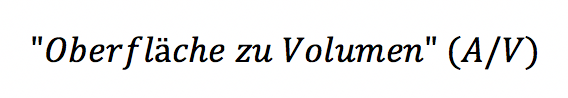
Den zugehörigen Wert finden Sie an letzter Position im vorgestellten Rechner. Es ergibt sich, indem Sie die Oberfläche A durch das Volumen dividieren.
Erklärungen zu den unterschiedlichen Kugeln und deren Radien beim Dodekaeder
Die noch verbleibenden drei Werte stellen unterschiedliche Radien dar. Hierbei handelt es sich um den Umkugel-, den Kanten- sowie den Inkugelradius. Der Umkugelradius bezieht sich gemäß der Namensgebung auf die Umkugel des Dodekaeders. Sie beschreibt eine virtuelle Kugel, die so ausfällt, dass sämtliche Ecken des Körpers darauf liegen. Der Mittelpunkt der besagten Kugel weist zu allen Ecken dieselbe Entfernung auf. Die entsprechende Distanz zwischen Mittelpunkt und einer der Ecken entspricht dem Umkugelradius. Die Formel für dessen Berechnung lautet:Mit der Kantenlänge von fünf Zentimetern aus dem Beispiel erhalten Sie ein Ergebnis von 7,006 Zentimetern.
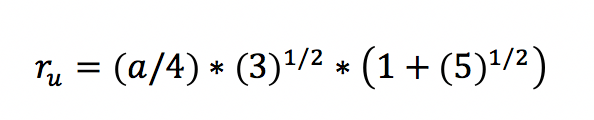
Der Kantenkugelradius fällt mit 6,545 Zentimetern etwas geringer aus. Hierbei greift die Formel:
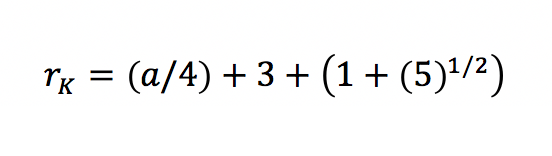
Im Unterschied zur Umkugel berührt die Kantenkugel nicht alle Ecken, sondern sämtliche Kanten des Dodekaeders. Der Berührungspunkt mit einer der Kanten befindet sich im Beispiel 6,545 Zentimeter vom Mittelpunkt der Kantenkugel entfernt.
Der Innenkugelradius bildet den niedrigsten Wert der drei Radien. Er ermittelt sich wie folgt:
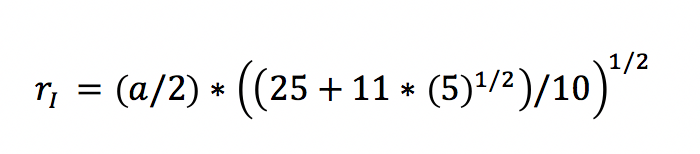
Wenn Sie das Dodekaeder berechnen, bekommen Sie hierfür einen Wert von 5,568 Zentimetern ausgewiesen. In der Raumgeometrie beschreibt die Inkugel einen runden Körper, der alle Flächen des Dodekaeders berührt. Erneut weist der Mittelpunkt der Kugel zu allen Begrenzungsflächen des platonischen Körpers den identischen Abstand auf.

