Transzendente Gleichung
Eine transzendente Gleichung können Sie mit dem Rechner von hilfreiche-tools spielend einfach online berechnen. Hier geht’s zur Online Berechnung.
transzendente Gleichung
Stell uns deine Frage. Wir antworten dir schnellstens...
Transzendente Gleichung berechnen
Da es sich bei der transzendenten Gleichung um einen wesentlichen Teil der Mathematik handelt, wird sie im Schulunterricht, aber auch während des Studiums gelehrt. Jedoch handelt es sich um eine komplexe Berechnung, deren Logik sich einem Großteil der Schüler nicht auf Anhieb erschließt, sodass sich die Rechnung als echte Herausforderung darstellen kann.
Damit Sie den schnellen Durchblick erhalten, worum es sich bei der transzendenten Gleichung handelt und wie diese berechnet wird, können Sie den Online-Rechner von hilfreiche-tools.de nutzen. Lassen Sie sich kinderleicht das korrekte Ergebnis ausrechnen oder nutzen Sie den Rechner, um zu überprüfen, ob Ihre eigenen Lösungswege korrekt sind.
Der Rechner für die Transzendente Gleichung
Um eine Transzendente-Gleichung zu lösen und zur korrekten Erkenntnis zu gelangen, geben Sie die benötigten Daten in den Rechner ein:
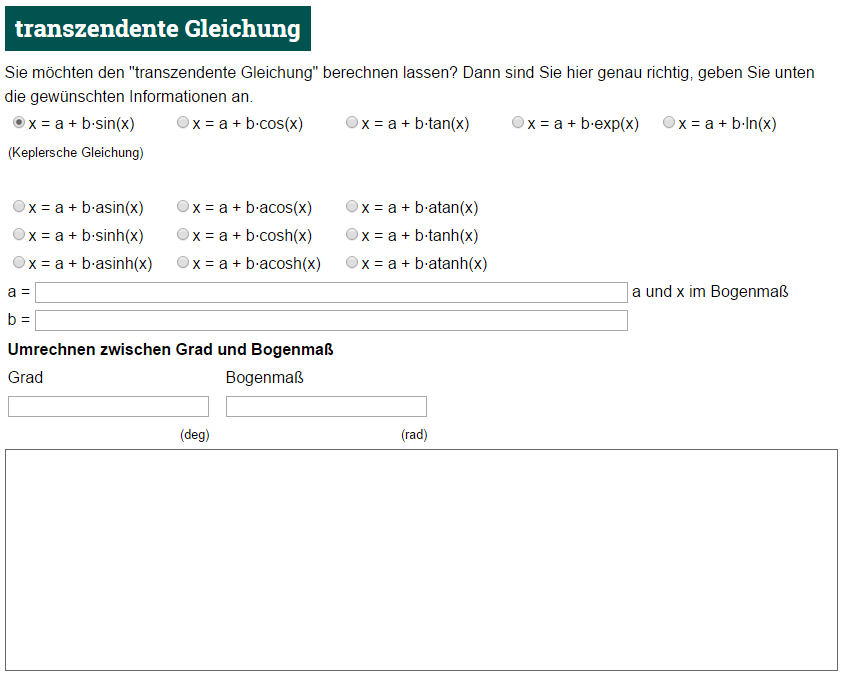
Klicken Sie danach auf „Berechnen“, damit das Ergebnis in Erscheinung tritt oder auf „Drucken“, um die Lösung auszudrucken.
Was ist ein Transzendent?
Die „8“ beispielsweise ist eine algebraische Zahl, für deren Berechnung die Algebra zum Einsatz kommt. Jedoch gibt es auch „nicht algebraische“ Zahlen. Dies bedeutet, dass der Transzendent nicht als Nullstelle des Polynoms mit ganzzahligen Koeffizienten ungleich dem Nullpolynom auftreten kann.
Ein Beispiel für einen Transzendent ist die Zahl Pi (?), deren Wert 3,1415926535897932384626433832795… beträgt.
(Quelle: Wikipedia)
Die Berechnung erfolgt mit Hilfe einer entsprechenden Formel, mit der sich beispielsweise eine lineare Funktion oder der Kreis in Mathe berechnen lassen.
Welche Gleichungen gibt es?
Man unterscheidet im Allgemeinen zwischen
Identischen Gleichungen
Bestimmungsgleichungen
Funktionsgleichungen
Bei einer Identität handelt es sich um eine Gleichung zwischen zwei Termen. Die Gleichung bleibt auch dann erhalten, wenn man anstatt der Symbole entsprechende Zahlenwerte einsetzt.
Beispiel für identische Gleichungen:
a (b+c) = ab + ac
Hingegen werden bei der Bestimmungsgleichung die sogenannten Unbekannten – die auch als „Variable“ bezeichnet werden – zunächst durch eine Berechnung ermittelt. Zum Ergebnis hat eine solche Gleichung eine Zahl oder einen Zahlenbereich. Diese Zahl wird als Lösungsmenge „L“ angegeben.
Beispiel für Bestimmungsgleichungen:
13 + x = 23
Lösung: x = 10
Lösungsmenge L = 10
Funktionsgleichungen dienen dazu, Zusammenhänge zwischen Größen herzustellen, die veränderlich sind, sodass beliebige Größen entstehen.
Beispiel für eine Funktionsgleichung:
Pi * d (Durchmesser) = U (Umfang)
Auch den Radius zu berechnen, ist mit einer Transzendent-Gleichung nicht unmöglich.
Bestimmungsgleichungen wiederum lassen sich in transzendente und algebraische Gleichungen unterteilen, wobei man im Bereich der Algebra lediglich multiplizieren, addieren, dividieren und subtrahieren sowie radizieren und potenzieren kann.
Hingegen handelt es sich bei einer transzendenten Gleichung um trigonometrische, logarithmische und exponentielle Gleichungen.
Beispiele für die Transzendenten-Gleichung:
x = a + b x cos (x)
x = a + b x In (x)
x = a + b x sin (x)
x = a + b x tan (x)
x = a + b x exp (x)
Cos = Cosinus
Sin = Sinus
Tan = Tangente
Das könnte Sie in diesem Zusammenhang auch interessieren:
Was bedeutet „Gravitation“?
Gravitation ist ein Begriff aus der Physik, welcher auch als „Schwerkraft“ bezeichnet wird und sich durch die Anziehung von Massen äußert, welche auf Gegenseitigkeit beruht. Das sogenannte Gravitationsfeld lässt sich mit Hilfe des Gravitationsgesetzes – welches durch Newton erfunden wurde – berechnen.
Was bedeutet „Matrix“ und „Iteration“?
Im Bereich der Mathematik bedeutet „Matrix“, dass mathematische Objekte in Form einer Tabelle angeordnet werden.
Die „Iteration“ bedeutet, dass man, um eine exakte Lösung zu finden, mehrfach dasselbe Rechenverfahren anwenden muss.
Was sind Umformungen und quadratische Gleichungen?
Quadratische Gleichungen sind Gleichungen nach folgendem Muster:
Ax² + bx² + c = 0
Spricht man von Umformungen, bedeutet dies, dass die Ausgangsgleichung in eine neue Gleichung umgewandelt werden kann. Jedoch muss durch Umwandlungen nicht nur die Ausgangsgleichung, sondern auch die neue erfüllt sein.
Was bedeuten „Kurve“ und „Kraft“ im Bereich der Mathematik?
Bei Kurven handelt es sich um eindimensionale Objekte, die durch verschiedene Gleichungen beschrieben werden können.
Im Bereich der Mathematik kann man die Kraft in zwei oder mehrere Teile zerlegen. Die Summe dieser Kräfte hat wiederum die gleiche Wirkung, wie es bei der unzerlegten Kraft der Fall ist. Beispielsweise können hier die Kräfte einer Ziege berechnet werden. Das daraus resultierende Ergebnis: Selbstverständlich werden mehrere Ziegen einen höheren Kraftaufwand erbringen, als ein einzelnes Tier.
Was bedeutet Grad in der Mathematik?
Mit Grad wird die Maßeinheit eines Winkels bzw. dessen Neigung angegeben. Die Höhe des jeweiligen Grades kann mit einer entsprechenden Formel berechnet werden. Schneiden sich zwei Geraden in einem rechten Winkel, bezeichnet man dies übrigens als „senkrecht“.
Was bedeutet „Anschauungsraum“?
Im Bereich der Mathematik ist der Raum eine Menge mit mathematischen Objekten. Diese weisen des Weiteren eine mathematische Struktur auf.
Was bedeutet „Teilchen“?
Teilchen ist ein Begriff aus der Physik, der unter anderem Atome sowie Moleküle beschreiben kann und im Rahmen der Teilchenphysik behandelt wird.
Viele den meisten Menschen unerklärliche, mathematischen Zusammenhänge wurden übrigens in den „Mathematischen Schriften“ von Leibniz festgehalten. Hierin finden Sie beispielsweise zahlreiche Informationen zu Gleichungen aller Art. Wenn Sie sich im Jahr 2016 weiterbilden möchten, können Sie dies jedoch auch kinderleicht mit unserem praktischen Rechner tun.

