Übersetzung Zahnradgetriebe berechnen
Hier können Sie die Übersetzung eines Zahnradgetriebes berechnen lassen. Geben Sie dazu unten einfach nur die Zähnezahl des antreibenen Rades sowie die Zähnezahl des angetriebenen Rades an.
z1=Zähnezahl des antreibenden Rades
z2=Zähnezahl des angetriebenen Rades
Stell uns deine Frage. Wir antworten dir schnellstens...
Was ist ein Zahnradgetriebe?
Zahnräder sind Räder, in deren Umfang Zähne eingearbeitet sind. Dank ihnen übertragen sie ein wirkendes Drehmoment auf ein anderes Zahnrad oder auf Ketten. Mehrere Zahnräder kombiniert bilden ein Getriebe. Dabei wirken zwei Räder mit der gleichen Kraft F aufeinander ein. Sie dienen zur Übertragung von zwei Drehungen oder einer Drehung und einer linearen Bewegung. Sie sind formschlüssig und somit schlupffrei. Die Zahnräder sind an Achsen befestigt oder auf Wellen gelagert. Sie bewegen sich zusammen mit ihnen und übertragen so die Drehungen und Bewegungen. Das Zahnradgetriebe berechnen Sie mithilfe des Rechners auf der Website.
Während die Räder sich bewegen, greifen die Zähne ineinander. Der Radabstand ist so groß, dass dies reibungslos geschieht. Für ein konstantes Übersetzungsverhältnis beginnt der nächste Eingriff, wenn der vorherige noch anhält. Der Formschluss geht dabei nicht verloren. Unter Beachtung der Verzahnungsgesetze ist die Form der Zähne nicht vorgeschrieben. Die Form am Gegenrand entspricht der Form der Eingriffsfläche.
Bei unterschiedlich großen Rädern verringert oder vergrößert sich die Drehzahl. Gleichzeitig verändert sich das Drehmoment, da die Übersetzungsverhältnisse sich verschieben. Der Zahnradgetriebe Rechner dient dazu, die Auswirkungen dessen praktisch festzustellen. In der Praxis sind die Zahnradformen einfach herstellbar. Die gern verwendeten Zykloiden- und Evolventenverzahnungen weisen im Gebrauch diverse Vorteile auf.
Geschichtliche Hintergründe
Die älteste Form des Zahnrades finden Sie bei altägyptischen Göpeln. Es ist ein Holzrad mit am Rand eingesteckten Pflöcken. Die Assyrer verwendeten bereits die Rolle, welche die Ägypter später übernahmen. Durch die Verbindung zweier Elemente entstand der Flaschenzug. In der frühen Geschichte finden sich diverse Erwähnungen von Zahnrädern. Die Bedeutendste ist für die heutigen Verhältnisse der Mechanismus von Antikythera von ungefähr 100 vor Christus.
In den Anfängen achteten die Konstrukteure kaum auf die Form der Zähne. Angaben von Gottfried Wilhelm Leibniz und Christiaan Huygens inspirierten den dänischen Astronom Ole Römer zur Empfehlung der Epizykloide als geeignete Form der Zähne. Ihre erste gründliche mathematische Untersuchung stammt von Philippe de La Hire und erschien 1730.
Die epizykloide Form sichert bei gleichmäßiger Gleitreibung eine gleichförmige Bewegung der Zahnräder. Sie fand gezielt in Uhrwerken Anwendung. 1759 entwickelte John Smeaton eine eigene Kreation. 1760 schlug Leonhard Euler die Evolvente für die Zahnung vor. Die verschiedenen Formen haben auf die Berechnung keinen Einfluss. Die Übersetzung Zahnradgetriebe berechnen Sie unabhängig von der Form mit der auf der Seite angegebenen Formel.
Der Bedarf an Zahnrädern stieg im 18. Jahrhundert mit der Einführung der Dampfmaschine. Anstatt wie bisher aus Holz entstanden Ausführungen aus Metall. Die Schräg- und Pfeilverzahnung ist eine Erfindung von Joseph Woollams aus dem Jahre 1820. Vier Jahre später baute James White daraus ein Differenzialgetriebe. Im 19. Jahrhundert erforderte der Werkzeug-Maschinenbau eine steigende Genauigkeit der Verzahnungen. 1887 baute G. Grant die erste brauchbare Maschine zum Fräsen von geradverzahnter Stirnräder. Heinrich Schicht entwickelte ab 1922 ein Verfahren zur Herstellung von Kegelrädern zur Serienreife.
Wo kommt das Zahnradgetriebe zum Einsatz?
Zahnradgetriebe übertragen Drehmomente schlupffrei und mit konstantem Übersetzungsverhältnis. Klassische Kfz-Getriebe bestehen aus Zahnrädern. Ein weiteres typisches Beispiel für die Paarung von Zahnrädern und Ketten ist die Fahrradkette. Die Kettenglieder greifen in die Zahnlücken und bestimmen die Gänge des Fahrrades. Dank eines Mechanismus ist die Übersetzung verstellbar, damit das Fahrrad auf geraden Strecken oder Steigungen einen angemessenen Kraftaufwand erfordert.
Unterschiedliche Zahnradarten
Es gibt verschiedene Zahnradarten auf dem Markt, die in verschiedenen Sparten zum Einsatz kommen. Die Zahnstange beispielsweise ist die Zahnschiene einer Zahnradbahn. Sie dient dazu, einen Zug durch die Kraftübertragung der Zahnräder an einen bestimmten Ort in einer höher gelegenen Region zu transportieren. Hier ist das Zahnradgetriebe berechnen eine wichtige Aufgabe, um Kraft und Last aufeinander abzustimmen. Die Zahnräder sind hier am richtigen Platz, da sie auf einfache Art und Weise die Kraft wirkungsvoll übertragen und damit große Lasten, sprich viele Personen, einen Berg hinauf transportieren.
Getriebe mit Ellipsenrädern sind bei Webmaschinen oder bei Fahrrädern gebräuchlich. Die Achsen von Kegelrädern schneiden sich bei 90 Grad. Es kommt beispielsweise in Automobilen oder Lokomotiven vor. Die Übertragung von Bewegung und Kraft findet winklig statt und das Getriebe verfügt über einen hohen Wirkungsgrad. Es ist wartungsarm und vorteilhaft für viele Konstruktionen.
Übersetzung Zahnradgetriebe berechnen – so funktioniert es
In einem funktionierenden Zahnradgetriebe passen die Zähne in ihrer Geometrie zusammen. Das Übersetzungsverhältnis entspricht der Anzahl der Zähne auf Abtriebsseite zur Anzahl beim Antrieb. Es gilt folgende Formel:

Die Übersetzung Zahnradgetriebe berechnen Sie anhand dieses Terms. Mehrstufige Getriebe kalkulieren Sie mit Verkettungen. Dabei verstehen Sie die Abtriebswelle der ersten Stufe als Antriebswelle des zweiten Levels. Die Methode dient zur Berechnung von unbegrenzten Kaskadierungen.
Wie funktioniert der Rechner?
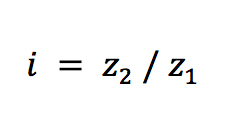
Z2 ist die Zähnezahl des angetriebenen Rades,Z1 diejenige des antreibenden. Der Zahnradgetriebe Rechner benötigt die beiden Angaben, um die Übersetzung zu berechnen. Sie geben beide Angaben in die entsprechenden Kästchen als eine positive Zahl ein. Verwechseln Sie die Begriffe nicht, da sie sich ähneln. Beim Klick auf das Feld „Berechnen“ erscheint das Resultat im Ergebnisrechteck.
Ein Berechnungsbeispiel
Die Antriebswelle des gegebenen Getriebes besitzt 48 Zähne, während die Abtriebswelle 96 Zähne beinhaltet. Nach der obengenannten Formel teilen Sie 96 durch 48, was zwei ergibt. Im Ergebnisrechteck erscheint folgendes Resultat:

Die reine Addition ergibt 2. Das andere Verhältnis entsteht dadurch, dass Sie das angetriebene Rad als eins annehmen. Im Verhältnis dazu besitzt in diesem Beispiel das antreibende Rad die Hälfte der Zähne des Ersteren. Daraus folgt das Verhältnis 1/0,50.
Wer benutzt den Zahnradgetriebe Rechner?
Im Maschinenbau tätige Personen wie Ingenieure, Zeichner und Metallarbeiter beschäftigen sich tagtäglich mit Getrieben und ihren Funktionen. Der Rechner bietet nützliche Informationen für Schüler und dient dazu, Aufgaben fürs Studium oder die Schule zu berechnen. Er eignet sich für einfache Aufgaben in Physik. Er ist gut zu bedienen und die Formel dahinter verstehen nicht nur Physik-Liebhaber. Das Verhältnis ist für alle Personen leicht verständlich.
Häufig gestellte Fragen
Was ist überhaupt ein Zahnradgetriebe?
Welche Arten von Zahnradgetrieben gibt es?
Wo werden Zahnradgetriebe eingesetzt?
Wie berechnet man die Übersetzung des Zahnradgetriebes?
Beispiel zur Berechnung des Zahnradgetriebes
Häufig gestellte Fragen
Was ist überhaupt ein Zahnradgetriebe?
Getriebe dienen primär der Anpassung von Drehzahlen zwischen Antrieb (zum Beispiel einem Motor) und Abtrieb (zum Beispiel einer Seilwinde). Je nach gewähltem Übersetzungsverhältnis (dem Verhältnis der Drehzahlen von Antrieb und Abtrieb) ergeben sich auch unterschiedliche Verhältnisse bei den Drehmomenten.
Bei „untersetzten“ Getrieben ist die Abtriebsdrehzahl geringer als die Antriebsdrehzahl, das Drehmoment ist dann am Abtrieb höher als auf der Antriebsseite.
Diese Anpassung von Antrieb und Abtrieb kann mit Hilfe verschiedener Technologien erfolgen. Bei einem Zahnradgetriebe wird diese Anpassung durch ineinandergreifende Zahnräder auf den beteiligten Wellen realisiert. Allen im Folgenden beschriebenen Variationen ist gemein, dass die Zahnabstände und -geometrien ungeachtet der unterschiedlichen Zahnraddurchmesser auf beiden Wellen aufeinander abgestimmt sein müssen.
Welche Arten von Zahnradgetrieben gibt es?
Je nach konstruktiven Rahmenbedingungen lassen sich verschiedene Arten von Zahnradgetrieben unterscheiden. Nachstehend sind die wichtigsten Arten und ihre Merkmale aufgeführt:
Stirnradgetriebe
Merkmal von Stirnradgetrieben sind parallel zueinander stehende An- und Abtriebswellen. Diese Getriebeart kommt vorwiegend in Maschinenantrieben zum Einsatz.
Kegelradgetriebe
Kegelradgetriebe sind dadurch gekennzeichnet, dass die Wellen nicht parallel zueinander, sondern in einem bestimmten, meist rechten Winkel zueinander angeordnet sind. Sie kommen dort zum Einsatz, wo neben einer Drehzahlanpassung bedingt durch bauliche Gegebenheiten auch eine Umlenkung der Rotationsbewegung erforderlich ist.
Schneckengetriebe
Schneckengetriebe als Sonderfall der Zahnradgetriebe weisen auf der Antriebswelle kein Zahnrad, sondern eine Schneckenkonstruktion auf, in die das Zahnrad der Abtriebswelle greift. Einsatz finden Schneckengetriebe für besonders hohe Untersetzungsverhältnisse bei langsam drehenden Abtrieben.
Zahnstangengetriebe
Ein weiterer Sonderfall ist das Zahnstangengetriebe. Bei dieser Bauart wird das Zahnrad auf der Abtriebswelle durch eine lineare Anordnung von Zähnen ersetzt wird. Dadurch lassen sich Drehbewegungen in lineare Bewegungen übersetzen, wie zum Beispiel bei Positioniertischen.
Planetengetriebe
Planetengetriebe sind meist im Kopfstück von Getriebemotoren zu finden. Bei ihnen stehen Antriebs- und Abtriebswelle in einer Flucht im Zentrum der Anordnung. Die Koppelung von Antrieb und Abtrieb erfolgt mindestens zweistufig durch planetenartig zwischen den Hauptzahnrädern auf An- und Abtrieb angeordnete Zahnräder.
Wo werden Zahnradgetriebe eingesetzt?
Zahnradgetriebe finden überall dort Anwendung, wo Drehmomente möglichst schlupffrei mit konstantem Übersetzungsverhältnis übertragen werden sollen. Dieses Übersetzungsverhältnis kann im Betrieb lediglich bei schaltbar ausgelegten Getrieben geändert werden, indem auf geeignetem Wege auf andere Zahnradpaarungen umgeschaltet wird.
Ein praktisches Anwendungbeispiel liegt in klassischen Kfz-Getrieben oder auch in Maschinen mit hohen Kraftmomenten wir Drahtzuganlagen. Auch Zahnradbahnen bedienen sich der Technologie der Zahnradgetriebe.
Wie berechnet man die Übersetzung des Zahnradgetriebes?
Es wurde eingangs bereits erwähnt, dass die Zahnradpaarungen hinsichtlich Geometrie der Zähne zusammen passen müssen. Ist dies gegeben, dann lässt sich das Übersetzungsverhältnis eines Zahnradgetriebes einfach über die Anzahl der Zähne auf antreibender Welle und Abtriebswelle ermitteln. Es gilt folgende Formel:
Antriebsdrehzahl / Abtriebsdrehzahl = Zahnzahl Abtriebsseite / Zahnzahl Antriebsseite
Bei mehrstufigen Getrieben erfolgt die Berechnung durch Verkettung. Das bedeutet, das die Abtriebswelle der ersten Stufe (vom Antrieb aus gesehen) als Antriebswelle der zweiten Stufe verstanden wird. Mit dieser Methode lassen sich unbegrenzte Kaskadierungen berechnen. Ein Beispiel für ein zweistufiges Zahnradgetriebe wird weiter unten berechnet.
Beispiel zur Berechnung des Zahnradgetriebes
Gegeben sei ein zweistufiges Zahnradgetriebe mit folgenden konstruktiven Parametern:
Antriebsdrehzahl: 1000 Umdrehungen / min
Zahnrad Antriebswelle: 48 Zähne
Zahnrad Zwischenwelle: 96 Zähne Antriebsseite / 24 Zähne Abtriebsseite
Zahnrad Abtriebswelle: 120 Zähne
Wie hoch ist die Drehzahl der Abtriebswelle?
Berechnung der 1. Stufe
Antriebsdrehzahl / Abtriebsdrehzahl = Zahnzahl Abtriebsseite / Zahnzahl Antriebsseite
Abtriebsdrehzahl = Antriebsdrehzahl / (Zahnzahl Abtriebsseite / Zahnzahl Antriebsseite)
Abtriebsdrehzahl = 1000 Umdrehungen pro Minute / (96 / 48)
Abtriebsdrehzahl = 500 Umdrehungen pro Minute
(dies ist die Drehzahl der Zwischenwelle!)
Berechnung der 2. Stufe
Antriebsdrehzahl / Abtriebsdrehzahl = Zahnzahl Abtriebsseite / Zahnzahl Antriebsseite
Abtriebsdrehzahl = Antriebsdrehzahl / (Zahnzahl Abtriebsseite / Zahnzahl Antriebsseite)
Abtriebsdrehzahl = 500 Umdrehungen pro Minute / (120 / 24)
Abtriebsdrehzahl = 100 Umdrehungen pro Minute
Die zweistufige Getriebekonstruktion stellt also eine Untersetzung von 10:1 dar.

