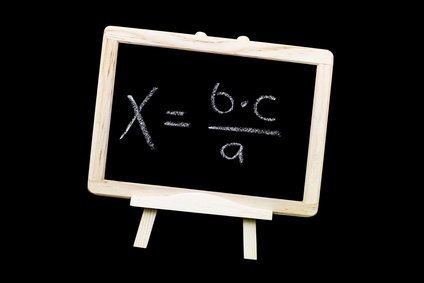Dreisatzrechnung
Dreisatz: Rechner und Erklärungen zu Rechenwegen
Wer den Dreisatz verstanden hat, wird schnell feststellen, dass es sich hierbei um ein einfaches Rechenverfahren der Mathematik handelt. Damit auch Sie von heute an mit der Dreisatzrechnung umgehen können, gehört es zu unserer Leistung, Ihnen zu erklären, wie der jeweilige Rechenweg funktioniert. Des Weiteren können Sie unseren praktischen Rechner nutzen, mit dem Sie das Ergebnis im Handumdrehen auch ohne Vorkenntnisse ermitteln.
Selbstverständlich liefern wir Ihnen Informationen, worum es sich bei der Rechenart handelt und welche Werte Sie in der Gleichung angeben müssen. Anhand von Beispielen veranschaulichen wir Ihnen, wie Sie die jeweilige Rechnung spielend einfach lösen. Verständlich wird beispielsweise erklärt, welche Zahlen, welche Größe oder welche Fläche multipliziert werden müssen, um die benötigte Zahl oder Gesamtfläche zu erhalten. Sie können den exakten Erläuterungen entnehmen, wie Sie im Einzelnen rechnen müssen, um auf das benötigte Ergebnis zu kommen.
Der Dreisatz – Jetzt den Dreisatz berechnen
Stell uns deine Frage. Wir antworten dir schnellstens...
Wie funktioniert die Dreisatzrechnung?
Mithilfe der Dreisatzrechnung, auch als Schlussrechnung oder kurz Schlüsse bekannt, werden drei gegebene Werte verglichen, die zueinander in einem bestimmten proportionalen Verhältnis stehen. Aus diesen Verhältnissen zueinander lässt sich der unbekannte vierte Wert ermitteln. Die Vorgangsweise der Berechnung bleibt stets dieselbe, das bedeutet, dass sich Dreisatz-Aufgaben durch Anwendung desselben Schemas einfach lösen lassen.
Der Dreisatz ist also ein Lösungsverfahren eines mathematischen Problems, das sich anwenden lässt, ohne die damit verbundenen mathematischen Gesetzmäßigkeiten vollständig zu kennen oder zu verstehen. Wichtig dabei ist, die grundsätzliche Gesetzmäßigkeit von Proportionen zu verstehen, um dem Schema dieser Berechnungsart zu folgen.
Um die Berechnungsart durch Verhältnisse oder Proportionen zu verstehen, kann man sich zunächst mit der einfacheren Variante namens Zweisatz beschäftigen, wo Rechenaufgaben durch einfache Proportionen gelöst werden. Beispiel: 2 Liter Milch kosten 1,50 Euro, wie viel kosten 5 Liter Milch?
Der Dreisatz im Video verständlich erklärt

Proportionale und antiproportionale Verhältnisse
Verhältnisse oder Proportionen sind in der Mathematik das um und auf, um fehlende Größen zu berechnen. Die Bezeichnung „Satz“ kommt vom alten deutschen Ausdruck „satzen“ für das Einsetzen der bekannten Größen in einer Gleichung.
Der einfache (oder verallgemeinerte) Dreisatz beruht auf einer direkten Proportionalität und folgt der Formel „A verhält sich zu B ebenso wie C zu X“
a : b = c : x
Wird diese Formel gemäß mathematischer Regeln umgestellt, ergibt sich:
x = c * b / a
Das bedeutet, die Werte stehen proportional zueinander, steigt der Wert A oder B, dann steigt auch der Wert bei C oder X.
Das Verhältnis der Werte zueinander kann auch antiproportional sein – wenn ein Wert erhöht wird, dann sinkt der andere Wert. Man denke da beispielsweise an eine Person, die zum Umgraben eines Gartenbeetes 1 Stunde benötigt. Wenn zwei Personen graben, benötigen sie für dasselbe Beet logischerweise nur die halbe Zeit. Dieses Werteverhältnis bezeichnet man auch als umgekehrten Dreisatz.
Der Hilfreiche Tools-Rechner ermöglicht es Ihnen, den Dreisatz sowohl in proportionalen als auch antiproportionalen Verhältnissen zu berechnen.
Worum handelt es sich beim Dreisatz?
Der Dreisatz wird hinsichtlich der Synonyme auch als „Berechnung zur Proportionalität“ oder „Verhältnisgleichung“ bezeichnet. Es handelt sich hierbei um ein mathematisches Verfahren, welches aus drei Werten besteht, aus denen ein Ergebnis ermittelt werden muss. Die Werte müssen in einem Verhältnis zueinander stehen, weshalb man von der „Verhältnis-gleichung“ spricht. Die leichteste Form ist die einfache Dreisatzberechnung (proportionaler Drei-Satz), die Sie in den unteren Schulklassen gelernt haben. Jedoch gibt es auch Erweiterungen (antiproportionaler Drei-Satz), die deutlich komplizierter sind.
(Quelle: Wikipedia)
Ziel der Dreisatzrechnung ist es, anhand dreier bekannter Werte einen vierten unbekannten zu ermitteln. Grundvoraussetzung, damit dies gelingt, ist die korrekte Zuordnung der elementaren Werte.
So nutzen Sie den Dreisatzrechner:
Nachfolgend möchten wir Ihnen erläutern, wie der Dreisatzrechner aufgebaut ist und wie Sie diesen anwenden:
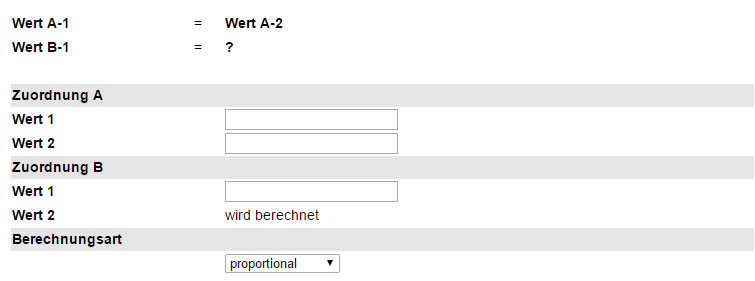
Indem Sie den Rechner in der Sprache Deutsch nutzen, können Sie innerhalb weniger Sekunden den fehlenden Wert ermitteln. Damit dies gelingt, tragen Sie die drei bekannten Werte korrekt in die jeweiligen Felder ein. Hierbei müssen Sie unbedingt die korrekte Zuordnung beachten, welche Ihnen über dem eigentlichen Rechner veranschaulicht wird:

Wert A1 ist grundsätzlich derjenige, dessen Sinnzusammenhang innerhalb der Dreisatzrechnung doppelt vorkommt. Den entsprechenden Relationswert tragen Sie in das Kästchen „Wert A2“ ein. In das Feld „Wert B1“ tragen Sie die Zahl ein, die mit Wert A1 übereinstimmt
Berechnungsbeispiel (Dreisatz Beispiel):
| 4 Büffel fressen 96 Kilo Gras. Wie viele Kilo fressen 6 Büffel?
|
|||
| Wert A1 | 4 | 4 Büffel | Sinnzusammenhängender, doppelter Wert |
| Wert A2 | 96 | 96 Kilo | Relationswert |
| Wert B1 | 6 | 6 Büffel | Mit „Wert A1“ übereinstimmender Wert |
| Wert B2 | wird berechnet | ||

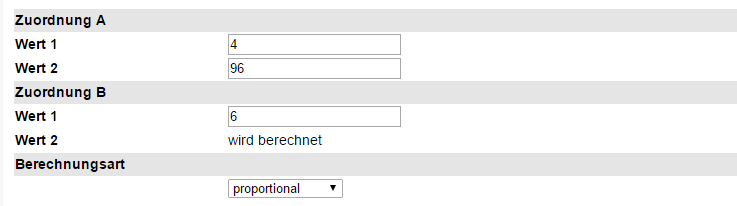
Indem Sie die Werte in die jeweilige Spalte eingeben und die Berechnungsart „proportional“ wählen, berechnen Sie umgehend das Ergebnis. Klicken Sie hierfür unterhalb des Berechnungsfensters auf die Schaltfläche „Berechnen“.
In der ersten Zeile des Berechnungsfensters erscheint nunmehr folgendes Ergebnis:

Indem Sie bei der Berechnungsart auf „antiproportional“ klicken, berechnet das System Ihnen die umgekehrte Aufgabe, ausgehend von folgendem Berechnungsbeispiel:
Büffel fressen 96 Kilo Gras. Wie viele Kilo fressen 4 Büffel?
Um diese Berechnung durchzuführen, müssen Sie daher nicht die Werte neu eingeben, sondern lediglich die Berechnungsart verändern. Sie erhalten in der ersten Zeile des Berechnungsfensters folgendes Ergebnis:

Wie erkenne ich, ob ich die Berechnungsart „proportional“ oder „antiproportional“ wählen muss?
Hierzu eine kleine Veranschaulichung:
| Proportional | Antiproportional |
| Steigen oder sinken beide Zuordnungen gleichermaßen, ist das Verhältnis proportional. | Steigt eine Zuordnung, während die andere sinkt, ergeben sich antiproportionale Verhältnisse. |
| Beispiel:
1 Kaffee kostet 2,00 € 2 Kaffee kosten 4,00 € 3 Kaffee kosten 6,00 € 4 Kaffee kosten 8,00 € |
Beispiel:
1 Person isst 500g Chips 2 Personen essen 250 g Chips 3 Personen essen 166,67 g Chips 4 Personen essen 125 g Chips |
Wer kann den Rechner für die Dreisatzrechnungen nutzen?
Jeder kann mit unserem hilfreichen Tool den Dreisatz berechnen. Es spielt keine Rolle, ob es sich um einen Schüler handelt, der die Dreisatzberechnung aktuell im Mathe Unterricht behandelt oder um einen Erwachsenen, der die Rechnung im täglichen Leben anwenden möchte. Die Verwendung des Tools gelingt kinderleicht. Viele Schüler nutzen es, um sich in Mathe – im Teilbereich Algebra – zu verbessern.
Worum handelt es sich beim verallgemeinerten Dreisatz?
Der verallgemeinerte Dreisatz verwendet Produkte einzelner Größen zur Verhältnisbildung:
| 4 Büffel fressen in 24 Stunden 96 kg Gras. Wie viele kg Gras fressen 3 Büffel in 7 Stunden? | |
| Die Berechnung erfolgt in wenigen Denkschritten: | Rechenweg |
|
|
|
96 kg : 4 Büffel = 24 kg je Büffel
24 kg : 24 Stunden = 1 kg je Stunde |
|
3 x 1 kg = 3 kg je Stunde
3 kg x 7 Stunden = 21 kg |
Umgekehrter Dreisatz: Was ist das?
Umgekehrter Dreisatz bedeutet, dass das Verhältnis nicht nach der gewünschten Proportionalität erfolgt, sondern sich umgekehrte Verhältnismäßigkeiten ergeben. Dies trifft unter anderem in folgenden Situationen zu:
- Je schneller das Auto fährt, desto weniger Zeit braucht es für die vorgegebene Strecke.
- Je mehr ich esse, desto langsamer schaffe ich den Bergaufstieg.
- Je mehr Geld ich in meine Versicherung einzahle, desto weniger Einkommen bleibt mir übrig.
Kann ich den Dreisatz auch für die Prozentrechnung anwenden?
Die Prozentrechnung kann selbstverständlich mittels Dreisatzaufgabe erfolgen. Die gesuchte Größe, die Sie bestimmen möchten, kann der Grundwert als auch der Prozentwert sein. Nachfolgend zwei Beispiele, wie Sie mit der Dreisatz-Aufgabe die Prozentrechnung durchführen:
| Suche nach dem Grundwert: | Berechnung |
| Beispiel:
Im Winterschlussverkauf erhalten Sie auf eine Jacke 40 % Rabatt. Sie kostet jetzt 80 Euro. Wie teuer war die Jacke vorher? |
60 % kosten somit 80 Euro. Wie viel die Jacke mit 100 % gekostet hat, soll errechnet werden
1 % = 80 Euro : 60 % = 1,33 Euro 100 % = 1,33 Euro x 100 = 133,33 Euro |
| Suche des Prozentwertes: | |
| Beispiel:
Wie viel sind 40 Prozent von 300 Euro? |
100 % = 300 Euro
1 % = 300 Euro : 100 % = 3,00 Euro 3,00 Euro x 40 % = 120 Euro
|
Häufig gestellte Fragen
Wie berechnet man den Dreisatz?
Häufig gestellte Fragen
Wie berechnet man den Dreisatz?
Der einfache Dreisatz wird in drei einfachen Denkschritten gelöst. Dabei werden zunächst zwei Behauptungen aufgestellt:
|
Größe A |
Größe B |
Kommentar |
|
X |
Y |
X und Y sind jeweils Mengen aus den Größen A und B |
|
1 |
X / Y |
Eine Einheit der Größe A wird mit X / Y gleichgesetzt |
|
Z |
Z * X / Y |
Z Einheiten der Größe A entsprechen Z mal X / Y Einheiten |
Zur Veranschaulichung seien folgende Beispiele gezeigt:
Preisberechnung von Waren
|
Menge |
Preis |
Kommentar |
|
5 kg |
10 EUR |
5kg Mehl kosten 10 EUR |
|
1 |
'10 / 5 EUR |
1 kg Mehl kostet 2 EUR |
|
3 |
3 * 10 / 5 EUR |
3 kg Mehl kosten 6 EUR |
Wegstrecke eines motorbetriebenen Förderbandes
|
Weg |
Drehzahl |
Kommentar |
|
10 m |
250 min-1 |
Bei 250 min-1 legt das Förderband 10 m pro Zeiteinheit zurück. |
|
1 m |
250 / 10 min-1 |
Für nur 1 m pro Zeiteinheit muss der Motor 25 min-1 drehen |
|
3 m |
3 * 250 / 10 min-1 |
Bei 3 m pro Zeiteinheit dreht der Motor mit 75 min-1. |
Kraftaufwand am Kran
|
Masse |
Kraft |
Kommentar |
|
10 kg |
100 N |
Zum heben von 10 kg werden 100 N aufgewendet. |
|
1 kg |
'100 / 10 N |
Für 1 kg sind 10 N aufzubringen |
|
3 kg |
3 * 100 / 10 N |
3 kg werden entsprechend durch 30 N gehoben. |